Arithmetic of the Medieval Universities
“Among the Greeks computation or reckoning, the arithmetic of business, was called logistic and was considered to be entirely different from the study of numbers as such, which philosophical study was called arithmetic” (page 266).
It is interesting to see that ancient Greek scholars have intentionally started to distinguish “applied mathematics” from “pure mathematics” by creating two different subjects called “logistic” and “arithmetic.” According to their standards, Euclid’s work The Elements which we studied in the history class is a representation of “arithmetic” because the content in the book is apparently not dealing with “sensible objects,” but rather a discussion of properties of numbers and proof.
“Throughout the Middle Ages, university instruction was based on a lecture-disputation method … There were no examinations in the modern sense of the term… To qualify for a degree, [the student] was required to participate in public disputations, either defending a proposition or opposing one defended by another student” (page 272).
I am surprised by the fact that the assessment in medieval universities was based on the public disputations instead of being hinged on the mark of examinations. This form of assessment reminds me of what I’ve learned in the assessment class; giving students an opportunity to defend their work is an essential part of an authentic assessment. I also begin to think why the present universities abandoned that way to evaluate whether students can be qualified for a degree.
“Recorde proposes for the painless use of Arabic numerals. For example, one need learn multiplication tables only as far as five times five if he chooses to multiply by Recorde’s method” (page 273).
It is the first time that I have seen this method, and I find it intriguing because this method not only provides us a “painless” approach to do multiplication without rote but also prompt me to think on why learning the history of mathematics can be helpful for both teachers and students. One of the reasons is that we may have unexpected gains while walking through the development of a mathematical idea. For instance, when we are looking at the history of arithmetical in university curricula, we may inadvertently find the link between the cross sign Recorde used in his multiplication method and the origin of x as a symbol of multiplication.
Work Cited:
Schrader, Dorothy V. "The Arithmetic of the Medieval Universities". The Mathematics Teacher. National Council of Teachers of Mathematics. pp. 264-278. https://drive.google.com/file/d/1EmwPVUkw8E1xjcON17spBNtuKITqYann/view
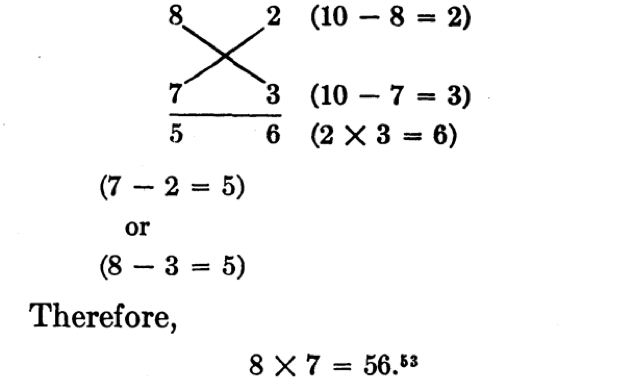

Great post!
ReplyDelete